Exercises II / 4.3
  1. For the standard normal distribution, find each of the following:
    1. P(0 < z < 1.24)
    2. P(-2.2 < z < 0)
    1. P(z > 0.5)
    2. P(z > -0.5)
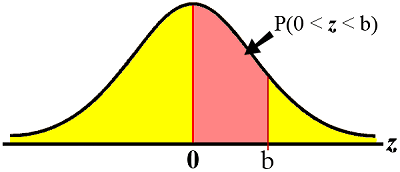
    Std. Normal Distribution graph / Exercises #1 & #2 (link: Reference 7 Table)
  2. For the standard normal distribution, find each of the following:
    1. P(-0.25 < z < 2)
    2. P(0.5 < z < 1.25)
    1. P(-2.33 < z < -1.25)
    2. P(z < -1.67)


    In each of the exercises below, the (population) data is either known or assumed to be normally distributed.

  3. The nicotine content of a particular brand of cigarette is found to have a mean of 2.25 mg and a standard deviation of 0.3 mg.  What percentage of the cigarettes will contain more than 2.5 mg?
  4. The Stanford-Binet Intelligence Test is designed and scored such that the mean IQ (i.e., "Intelligence Quotient") of individuals is 100 while the standard deviation is 16.  What percent of persons tested should be expected to have an IQ of 120 or higher?

  5. The magnitude distribution for major earthquakes in California (CA) over the past 100 years has a mean of 6.2 (on the Richter scale) and a standard deviation of 0.5.  Determine each of the following:
    1. What percent of CA earthquakes can be expected to be magnitude 7.0 or higher?
    2. What percentage would be expected to have a magnitude of 6.0 or less? 
  6. A nation-wide survey determined that an adult watches an average of 18.6 hours of tv per week in the U.S.  If the standard deviation is 2.3 hrs, then what percent of American adults watch between 15.0 and 20.0 hours of television per week?

  7. A study of the weights for newly-born babies found that the mean was 3400 grams and that the standard deviation was 505 g.  What percent of newly-born babies will have a birth-weight of more than 8 pounds?

  8. The median life of a certain brand of tires is 30,000 miles and they have a standard deviation of 2000 miles.  If the manufacturer sells 50,000 tires, how many will last:
    1. less than 30,000 miles?
    2. less than 35,000 miles?
    3. more than 35,000 miles?
    4. between 30,000 miles and 35,000 miles?
    5. between 27,500 miles and 32,500 miles?


  9. If the average adult's resting heart rate is 68 beats per minute with a standard deviation of 4 beats per minute, then determine how many individuals in a survey of 80 adults you would expect to have a (resting) heart rate of 75 or less beats per minute.

  10. Radar is used to check the speed of traffic on Interstate 75 north of Atlanta.  If the mean speed of the traffic is 60 mph, and the standard deviation is 4.25 mph, then approximately how many cars out of every one-hundred are actually obeying the legal speed limit of 55 mph along this stretch of highway?
     
  11. In order to qualify for police training, recruits are given a test of stress tolerance.  The test scores are tabulated and the data set has a mean of 60 and a standard deviation of 10.  If only the top 20% of the recruits are to be selected, then what will the test's cut-off score need to be?

  12. A state realty-licensing board gave an exam assessing the math skills of realtors.  The exam had a mean score of 72 and a standard deviation of 12.
    1. The top 10% are to receive a special certificate.  What minimum score must the realtor make in order to receive the certificate?
    2. The bottom 25% are to be required to attend a remedial workshop.  What minimum score would a realtor need to avoid having to take the workshop?

  13. Market research conducted by Proctor & Gamble reported that a typical American family of four washes an average of one ton of clothing every year, and that the standard deviation is 200 pounds.  The middle 50% of these families wash an amount of clothing which falls between what two values?  Express the answers rounded to the nearest whole pound.

  14. An instructor gives a 100-point exam which after grading is found to have a mean score of 60 and a standard deviation of 13.
    1. What percentage of the students score less than 60?
    2. What percentage of the students score more than 70?
    3. What percentage of the students score between 65 and 75?
    4. Find the scores which will divide the distribution into the following categories:
      Letter Grade Percent of Students
      A 5%
      B15%
      C60%
      D15%
      F 5%
  15. Repeat the exercise above for an exam in which the mean score is 65 and has a standard deviation of 10 points.