can consider it a notable achievement.  It isn't exactly the be-all, end-all of mathematical accomplishments but it is quite a fundamental standard by which anyone's quantitative literacy is benchmarked (even outside of or beyond this course).  With this said, let's move on to one last yet more elaborate example where several of our ideas combine in order to solve a problem involving what's commonly known as a composite figure. * * * 

Example 5

---

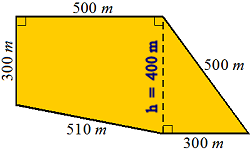
Find the Area, in hectares (ha), for the property shown in the illustration.  Hint: use the equivalence that 1 ha = 10,000 m².      The first realization that needs to occur is that the property consists of two simple figures, a trapezoid (on the left) and a right triangle (on the right).  With this in mind, one may proceed to find the Area of each piece separately and then add them together to find the total Area of the entire figure / property.  The length of the dashed

vertical line (i.e., the height of the right triangle) is unknown, which is also a key dimension to the trapezoid.  Thus, the first calculation will be to determine this quantity (as it is needed in order for us to obtain the Area for either of the two simple figures) via Pythagoras:

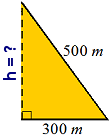
h

²

+

(

300 m

)

²

=

(

500 m

)

²

h

²

+

90,000 m²

=

250,000 m²

h

²

=

250,000 m²

-

90,000 m²

h

²

=

160,000 m²

h

=

√160,000    m²

h

=

400 m

And the picture now looks like...