Page 10

     Checking back with Example 1 will show a consistent result for the triangle's Area using the conventional formula as one ought to expect.  Successful completion of our third example ought to have boosted our confidence and morale to the point where we are adequately prepared to tackle the much heralded Pythagorean Theorem?
* * * 
 PYTHAGOREAN THEOREM  *
     Given a right triangle, with legs (the two shorter sides) of length "a & b" and whose hypotenuse  (the longest side,  opposite the right
Right Triangle diagram
angle) being of length "c," then the relationship between the three sides is to be determined by the Pythagorean Theorem:
a² + b²  =  c²
     Seems as good a time as any to give this concept a whirl.  Example 4 does just that (press onward courageous reader)...
 

  • Example 4
    Find the length of the unknown side for the triangle shown in the illustration.
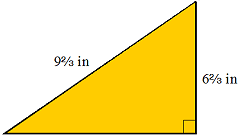
    Example 4: right triangle diagram
         The length of the bottom side is not known, so let's label it as the unknown "b" (i.e., the base of the triangle), and then employ the Pythagorean Theorem where a =  623cm (length of the given leg) and c = 923cm (length of the hypotenuse) as follows: 
    ( 623in ) ²  +  b ²   =   ( 923in ) ²  
    4449in²  +  b ²   =     9349in²  
      b ²   =     9349in²  -   4449in²
      b ²   =     49 in²
      b   =   √49      in²
      b   =    7 in  
         Once one grasps what has happened here, you
    • * The importance of this mathematical formula is difficult to overemphasize as it will be a necessity for a significant number
        of problems throughout the remainder of the course/text.
    < Previous Page   Next Page >