We have a little more to discuss about triangles. First, there is an alternative formula for finding the Area of a triangle when all three sides are known (and the height may not be known).  Second comes the most infamous of all mathematical formulas since antiquity.  Any idea of what equation that may be?  It relates the three sides of a right triangle.  If you still don't know, hang tight, we'll get to it shortly. * * *      Whenever the three sides of a triangle are given the Area may be found by using an equation known as Heron's formula. If the lengths of the three sides of a triangle are a, b, & c, then the Area of the triangle is given by the formula:

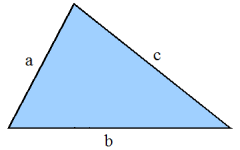
A  =  √s(s - a)(s - b)(s - c)
where  s =12P  (semiperimeter)

   Clearly this equation may look a bit daunting. However, once you understand what "s" is (i.e., the semiperimeter), then it's really nothing more than a little bit of arithmetic.

Example 3

---

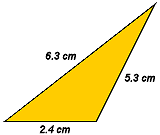
Find the Area of a triangle with the dimensions shown in the illustration.      Since the triangle's height is unknown (and unascertainable

unascertainable (adj.):  un-ass-sur-tAne-uh-bull incapable of being determined or discovered; not able to establish, achieve or acquire

within the scope of our mortal mathematical prowess

prowess (n.):  prow-uhss a superior ability acquired through practice and observation; adroitness or dexterity in a particular skill

at this stage), we are forced to resort to using Heron's formula.  The semiperimeter is needed before we have all the information needed to substitute into the suspect (square root) formula.  So,

s  =	1 2 (6.3 cm + 2.4 cm + 5.3 cm)
=	1 2 (14 cm)
=	7 cm

All that's left is to plug in the four quantities (a, b, c & s) and go about simplifying the resulting arithmetic expression:

A =	√7cm(7cm - 6.3cm)(7cm - 2.4cm)(7cm - 5.3cm)
=	√7cm(0.7cm)(4.6cm)(1.7cm)
=	√38.318cm  4
=	√38.318  × √cm  4
≈	6.2 cm²

---