Example 1

---

Find the Perimeter and the Area of the figure shown in the illustration.      First up, the Perimeter is found by adding the (three) sides (of the triangle):

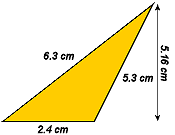
P  =	6.3 cm + 2.4 cm + 5.3 cm
=	14.0 cm

     Lastly, finding the Area requires recognizing that the base is b = 2.4 cm long while the height is h = 5.16 cm high.  Subsequently, one obtains:

A  =	12 × 2.4 cm × 5.16 cm
=	1.2 cm × 5.16 cm
=	6.192 cm²
≈	6.2 cm²

---

     Moving beyond this first example (above), which hopefully demonstrates that there is little to fear with polygons, does however still leave us vulnerable to not appreciating the subsequent

level of complexity which is involved in coping with circular figures.  The next example will serve to illustrate how even this less familiar problem is well within our humble capabilities.

Example 2

---

Find the Circumference and the Area of a circle whose diameter is 2π in. 
     Although not absolutely necessary, let's find the circle's radius before doing anything else: r  = 12 ×2π in  = 1π in  The distance (Circumference) around this circle can be found using the formula C = 2πr; meaning we should calculate it as follows:

C  =	2π(1π in)	=	2 in

Finally, we can compute the Area using A = πr2:

A  =	π(1π in)²
=	π1( 1 π²in²)
=	1 π in ²        (exact)
≈	0.32in²    (approx.)

---

     Both an exact and an approximate answer are given above (Example 2).  Since the instructions did not designate which type of answer value should be stated, then either answer suffices as a correct one.