proportion to solve a typical problem.

Example 2
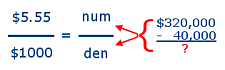
The (annual) homeowner's property tax rate for Hawaii County is $5.55 per $1000 of its taxable value, which is the "assessed" value less a $40,000 exemption.  If a property is assessed a value of $320,000 then what is the (yearly) amount of property tax to be levied upon the homeowner(s)?
First, let's use the tax rate $5.55/$1000 (or 0.0055) as the left-hand side of our proportion. Then, noticing that the numerator is the amount of tax — while the denominator is the taxable value, we'll need to set up the ratio on the right-side with $280,000 (i.e., $320,000 - $40,000) in which component of the fraction? Hopefully, you surmise that it will have to be placed in the denominator (as both ratios must correspond in format).  Once these aspects of the problem are realized, one now has the following equation (simplified proportion) to solve: Next, we'll multiply (both sides of the equation) by $280,000.  The right-hand simplifies down to

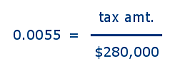the quantity we are attempting to find, which can be computed exactly by doing the arithmetic on the left-hand side...

---

     Looking back, notice each of the basic steps mentioned earlier.  First came the identification of one of the ratios involved (i.e., the tax rate). Secondly, determining another quantity (i.e, the taxable value) whose position in the other ratio needs to be recognized, and finally the (anti-climatic) arithmetic solution... Not so terribly complicated, yeah?  And maybe even just within the scope of YOUR very own seemingly limited logical powers of deduction!

SCALE      The use of scale is one of the more practical uses for fractions (ratios or rates).  Most people probably associate a scale with maps, but it is utilized in many other settings as well.  Models and (building) blueprints are two very common applications of scale.  In general, scale is simply a comparative resizing of some physical quantity whose actual size is not convenient or possible) to view or comprehend.  Shrinking or expanding the real-life dimensions of an object under study to a simulated size, one that makes its attributes or properties more easily accessible to a human's