| Example 1 (continued) |
denominator are different (i.e., ounces versus grams). The key here is to convert one of the units to the other.
For example, we (arbitrarily)
choose to convert the unit of grams into ounces using the approximate equivalence
between 28.4 grams and 1 ounce. The conversion rate can be written as:
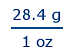

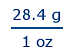

us to conclude that...
* * *
PROPORTION
A proportion is merely defined as the equality of two ratios, A/B = C/D. Knowing any three of the four quantities (A, B, C, and D) means that the unknown fourth quantity can be determined without much fuss. Our interest in proportions is that typically one of the ratios, either A/B or C/D, will be a known rate and also one of the remaining amounts (numerator or denominator) in the other ratio (rate) will be given, at which point our standard task is to go about determining the mystery quantity. This is somewhat of an oversimplification, since most problems require us to recognize both a known rate (say, A/B) along with yet another quantity (either C or D) from a brief written description of the problem, in addition to being able to assemble a suitable proportion before actually getting down to the business of solving it.
If the above is a little too abstract for you to completely follow, then the next example may help to illustrate the general nature of utilizing a
|
Purchasing a bag of Doritos @
14.1¢/oz is more economical than a bag of Tostitos @
17.2¢/oz — by about 3 cents per ounce.
|
|---|
A proportion is merely defined as the equality of two ratios, A/B = C/D. Knowing any three of the four quantities (A, B, C, and D) means that the unknown fourth quantity can be determined without much fuss. Our interest in proportions is that typically one of the ratios, either A/B or C/D, will be a known rate and also one of the remaining amounts (numerator or denominator) in the other ratio (rate) will be given, at which point our standard task is to go about determining the mystery quantity. This is somewhat of an oversimplification, since most problems require us to recognize both a known rate (say, A/B) along with yet another quantity (either C or D) from a brief written description of the problem, in addition to being able to assemble a suitable proportion before actually getting down to the business of solving it.
If the above is a little too abstract for you to completely follow, then the next example may help to illustrate the general nature of utilizing a